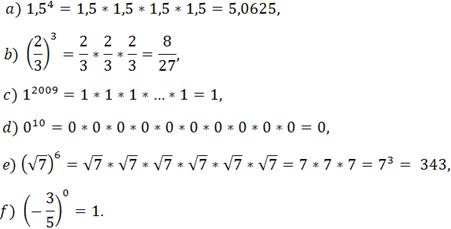MATEMATYKA

Nauka dostarczająca narzędzi do otrzymywania ścisłych wniosków z przyjętych założeń, zatem dotycząca prawidłowości rozumowania.

Ponieważ ścisłe założenia mogą dotyczyć najróżniejszych dziedzin myśli ludzkiej, a muszą być czynione w naukach ścisłych, technice a nawet w naukach humanistycznych, zakres matematyki jest szeroki i stale się powiększa.

Wiele dziedzin nauki i technologii, w pewnym momencie zaczyna definiować swoje pojęcia z dostatecznie dużą precyzją, aby można było stosować do nich metody matematyczne, co często zapoczątkowuje kolejny dział matematyki teoretycznej lub stosowanej.

Tak stało się np. z mechaniką klasyczną, mechaniką statystyczną, ekonomią (ekonometria), lingwistyką (lingwistyka matematyczna), teorią gier, a nawet niektórymi działami politologii (teoria głosowań).

Obecnie standardem w naukach eksperymentalnych jest potwierdzanie istnienia obserwowanych zależności za pomocą metod statystyki, będącej działem matematyki.

Pozwala to odróżnić rzeczywiste wyniki od przypadkowej zbieżności. Leonardo da Vinci stwierdził w Traktacie o malarstwie: „Żadne ludzkie badania nie mogą być nazywane prawdziwą nauką, jeśli nie mogą być zademonstrowane matematycznie.”

Matematyka teoretyczna, nazywana czasami matematyką czystą, jest często rozwijana bez wyraźnego związku z konkretnymi zastosowaniami.

W tej odmianie jest ona przez niektórych matematyków uważana za formę sztuki.

Jednak niektóre działy matematyki teoretycznej znalazły swoje praktyczne zastosowanie, kiedy okazało się, że potrzebuje ich nowoczesna fizyka lub informatyka.

Szkolne rozumienie matematyki, jako nauki wyłącznie o liczbach i pojęciach geometrycznych, zdezaktualizowało się już w XIX wieku wraz z postępami algebry i teorii mnogości. Częścią nieodzowną matematyki jest logika.

2.Definicje i wizje.

Paul Dirac stwierdził „Matematyka jest narzędziem stworzonym specjalnie do wszelkich abstrakcyjnych koncepcji, i nie ma ograniczeń dla jej potęgi w tym zakresie”

Benjamin Peirce nazwał ją „nauką, która wyciąga właściwe wnioski”

Henri Poincaré określił matematykę jako „sztukę nadawania takich samych nazw różnym rzeczom”

Oddaje to jedną z piękniejszych cech matematyki, zdolnej uogólniać właściwości i czynić analogie między bardzo odległymi i wydawałoby się mało ze sobą związanymi obiektami.

David Hilbert uznał, że „sztuka uprawiania matematyki zawiera się w znajdowaniu szczególnych przypadków, które zawierają w sobie zalążki uogólnień”

Poeta William Wordsworth stwierdził: „Matematyka jest niezależnym światem stworzonym przez czystą inteligencję”

Z czasem niektóre działy matematyki stały się odrębnymi światami, uprawianymi wyłącznie dla ich piękna, bez jakiegokolwiek związku z rzeczywistością.

Henry John Stephen Smith stwierdził wprost „Czysta matematyka, oby nigdy nie była przez nikogo używana”

Z drugiej strony Nikołaj Łobaczewski uznał, że „Nie ma gałęzi matematyki, choćby nie wiem jak abstrakcyjnej, która pewnego dnia nie zostałaby zastosowana do zjawisk realnego świata”

Wyprzedził tą wypowiedzią o pół wieku postępy fizyki, która stosuje w praktyce działy matematyki, przed jej epoką uważane za domenę czystej myśli, niezbrukanej zastosowaniami.

Immanuel Kant stwierdził „Matematyka jest najjaskrawszym przykładem, jak czysty rozum może skutecznie rozszerzać swoją domenę bez jakiejkolwiek pomocy doświadczenia”

3. Główne działy.

Matematyka jest dynamiczną symbiozą dziedzin, działów czy teorii, które przenikają się oraz zależą jedne od drugich.

Powstają wciąż nowe teorie, stare obumierają, a czasem znowu wracają do życia.

Matematyka wymyka się klasyfikacji lub zmusza do tworzenia klasyfikacji wciąż na nowo.

Amerykańskie Towarzystwo Matematyczne prowadzi klasyfikację gałęzi matematyki, w których prowadzone są aktywne badania naukowe.

Ta klasyfikacja jest uaktualniana co pewien czas aby odzwierciedlić zmiany w zainteresowaniach matematyków, a dzisiaj obowiązująca jej wersja jest określana jako MSC 2000 (Mathematical Subject Classification 2000)

MSC jest używane przez wiele czasopism matematycznych oraz baz danych w rodzaju Mathematical Reviews.

Klasyfikacja ta obejmuje opisane poniżej główne gałęzie matematyki, z których każda jest dalej dzielona.

Łącznie zawiera ona ponad 5000 szczegółowych dziedzin matematyki i dziedzin z matematyką związanych. Każda dziedzina ma przypisany pięcioznakowy kod.

4.GEOMETRIA

Dziedzina matematyki badająca dla wybranych przekształceń ich niezmienniki, od najprostszych,takich jak odległość, pole powierzchni,

miara kąta, przez bardziej zaawansowane, jak krzywizna, punkt stały, czy wymiar.

W zależności od rodzaju przekształceń mówi się o różnych rodzajach geometrii.

Geometria euklidesowa zajmuje się przede wszystkim badaniem niezmienników izometrii (zachowanie odległości)

oraz podobieństw (zachowanie kątów), geometria afiniczna bada niezmienniki przekształceń afinicznych,

zaś geometria rzutowa opisuje niezmienniki przekształceń rzutowych.

Problemy te uogólnia się na inne przestrzenie i obiekty (np. przestrzeń Riemanna, czy przestrzenie metryczne),

a metoda badania niezmienników jest podstawową metodą badania bardziej zaawansowanych obiektów matematycznych

(np. przestrzenie topologiczne, abstrakcyjne grupy, pierścienie, itp.)

Geometria, podobnie jak arytmetyka należy do jednych z najstarszych nauk.

Podobnie jak inne działy matematyki geometria wyewoluowała od badania kształtów znanych z codziennego życia

do studiów nad nieskończenie wymiarowymi abstrakcyjnymi przestrzeniami matematycznymi.

5.POTĘGOWANIE

Działanie dwuargumentowe będące uogólnieniem wielokrotnego mnożenia elementu przez siebie.

Potęgowany element nazywa się podstawą, zaś liczba mnożeń, zapisywana zwykle w indeksie górnym po prawej stronie podstawy, nosi nazwę wykładnika.

Wynik potęgowania to potęga elementu.

Na przykład:

3⁴= 3*3*3*3=81

gdzie podstawą potęgi jest liczba 3, a wykładnikiem liczba 4.

Drugą potęgę nazywa się często kwadratem, a trzecią – sześcianem (zwykle w stosunku do wartości liczbowych, choć nie tylko).

Określenia te nawiązują do geometrii, gdyż pole powierzchni kwadratu o boku długości a wynosi a², a objętość sześcianu o tym samym boku jest równa a³.

ZASTOSOWANIE :

Potęgi liczby 10 to liczby kończące się pewną liczbą zer. Dla skrócenia ich zapisu stosuje się tzw. przedrostki układu SI, w szczególności w notacji naukowej do zapisywania wielkich liczb i wielkości fizycznych.

Z racji konstrukcji współczesnych komputerów w informatyce często spotyka się potęgi liczby 2.

Na przykład 2n jest liczbą możliwych wartości zmiennej składającej się z n bitów (każdy bit może mieć wartość 0 lub 1, razem jest ich n).

Z tego powodu zwykle operuje się też wielokrotnościami liczby 2 (bądź jej pewnej potęgi).

Osiem bitów tworzy oktet (lub bajt), szesnaście – słowo.

Większe wartości również są wielokrotnościami liczby 2, nie zaś 10, jak wskazywałyby ich nazwy, np. kilobajt to 1 024, a nie 1 000 bajtów (Dla odróżnienia tych wielkości opracowano tzw. przedrostki dwójkowe).

Funkcji wykładnicza exp, czyli funkcja wykładnicza o podstawie e, jest szeroko stosowana w matematyce, pojawiając się szczególnie często w analizie matematycznej czy rachunku prawdopodobieństwa.

Potęgowanie modulo jest używane w kryptografii, np. w algorytmie RSA.

6.ALGEBRA

Jeden z najstarszych działów matematyki powstały już w starożytności.

Zajmuje się on strukturami algebraicznymi i relacjami.

Algebra elementarna zajmuje się takimi działaniami jak dodawanie i mnożenie; wprowadza pojęcie zmiennej i wielomianu razem z jego faktoryzacją i znajdowaniem ich pierwiastków,

jednakże algebra jest działem bardziej ogólnym (patrz podział algebry).

7.FUNKCJE

W matematyce dla danych dwóch zbiorów „przyporządkowanie” każdemu elementowi pierwszego zbioru dokładnie jednego elementu drugiego zbioru.

Ściśle funkcję definiuje się jako taką relację pomiędzy elementami dziedziny (pierwszego zbioru) a elementami przeciwdziedziny (drugiego zbioru),

dla której każdy element dziedziny jest w relacji z dokładnie jednym elementem przeciwdziedziny.

W matematyce określenia funkcja, przekształcenie, odwzorowanie, transformacja, operator, działanie, itd. są zwykle synonimami.

Jednakże w różnych dyscyplinach matematycznych preferowane jest używanie niektórych z nich, znaczenie niektórych zostało zaś zawężone.

Użycie konkretnej nazwy podyktowane jest dzisiaj przede wszystkim względami historycznymi.

Choć w analizie matematycznej rozpatruje się przede wszystkim funkcje, to w geometrii, algebrze liniowej mówi się o przekształceniach (przekształceniach liniowych

w algebrze uniwersalnej rozważa się z kolei działania, zaś w analizie funkcjonalnej bada się własności operatorów, czy funkcjonałów.

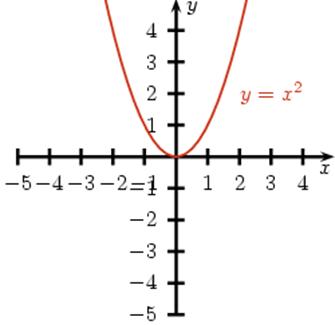
Powyższa zależność jest więc przykładem funkcji, która dalej będzie oznaczana literą f.

Zmienne niezależne danej funkcji nazywa się argumentami, w tym wypadku jest to zmienna x,

zaś uzyskana na ich podstawie zmienna zależna nazywana jest wartością funkcji, tutaj jest to zmienna y,

którą dla zaznaczenia zależności funkcyjnej f od zmiennej x oznacza się f(x) (czyt. „ef od iks”).

Przy często używanych funkcjach, jeśli nie sprawia to problemów, nawias zwykle pomija się: sinx lub lnx.

W niektórych wypadkach symbol funkcji pisze się po argumencie,

np. n! (czyt. „en silnia”). Tak więc dla argumentu 5 wartością funkcji f jest 10, co można zapisać f(5) = 10.

Dziedziną funkcji nazywa się zbiór wszystkich argumentów, a zbiorem wartości (obrazem) zbiór wszystkich wartości przyjmowanych przez funkcję;

w powyższym przykładzie dziedziną jest zbiór liczb całkowitych, a zbiorem wartości zbiór liczb parzystych.

Często wymaga się podania przeciwdziedziny, która zawiera zbiór wartości, lecz nie musi być mu równa.

W niektórych źródłach, wyraz „przeciwdziedzina” uważa się za synonim słowa „zbiór wartości”, w innych zaś nie –

dlatego w matematyce wyższej nie używa się terminu „zbiór wartości” wykorzystując w zamian termin „obraz” (zob. niżej).

Przyjęcie w podanym przykładzie za przeciwdziedzinę zbioru liczb całkowitych wykluczy ze zbioru wartości liczby nieparzyste.

8.PROCENTY

W matematyce sposób wyrażenia liczby jako ułamka o mianowniku 100, zwykle oznaczany symbolem %, np. 45% (czyt. „czterdzieści pięć procent”) oznacza \tfrac{45}{100} lu

Procenty umożliwiają wygodne wyrażenie danej wielkości w stosunku do innej, przy czym pierwsza wielkość oznacza zwykle część lub zmianę w drugiej.

Choć procenty wykorzystuje się zwykle do wyrażania liczb z zakresu od zera do jedynki, to można za ich pomocą wyrazić dowolną proporcję bezwymiarową.

Przykładowo 111% to 1,11, zaś − 0,35% oznacza − 0,0035.

Znak % nie jest skrótem jednostki miary. 5% z długości będzie wyrażone w metrach, a 5% z masy w kilogramach. Metr i kilogram to jednostki, a % to tylko mnożnik.

Mimo to niekiedy dla oznaczenia, że wynik pewnych obliczeń należy wyrazić w procentach, stosuje się zapis:

x=…* 100%

Jest to tylko umowna konwencja sugerująca zapis procentowy.

Z matematycznego bowiem punktu widzenia mnożenie przez 100% jest równoważne mnożeniu przez 1, czyli nic nie zmienia.

9.TWIERDZENIE PITAGORASA

Twierdzenie geometrii euklidesowej, które w zachodnioeuropejskim kręgu kulturowym przypisywane jest żyjącemu w VI wieku p.n.e. greckiemu matematykowi i filozofowi Pitagorasowi, chociaż niemal pewne jest, że znali je przed nim starożytni Egipcjanie.

Wiadomo też, że jeszcze przed Pitagorasem znano je w starożytnych Chinach, Indiach i Babilonii.

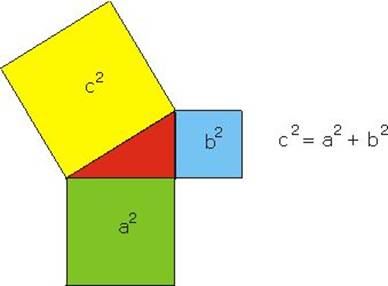
W dowolnym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej tego trój

a² + b²= c²

Geometrycznie oznacza to, że jeżeli na bokach trójkąta prostokątnego zbudujemy kwadraty,

to suma pól kwadratów zbudowanych na przyprostokątnych tego trójkąta będzie równa polu kwadratu

zbudowanego na przeciwprostokątnej.

W sytuacji na rysunku obok: suma pól kwadratów "czerwonego" i "niebieskiego" jest równa polu kwadratu "fioletowego".

10.TWIERDZENIE TALESA

Jedno z najważniejszych twierdzeń geometrii euklidesowej. Tradycja przypisuje jego sformułowanie Talesowi z Miletu.

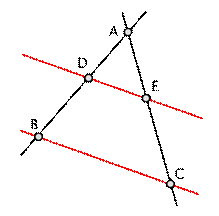
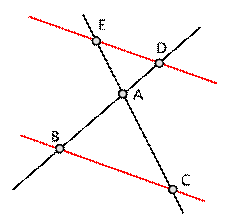
Jeżeli ramiona kąta przecięte są prostymi równoległymi, to odcinki wyznaczone przez te proste na jednym ramieniu kąta, są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta.


	$\frac{\|AD\|}{\|AE\|}=\frac{\|DB\|}{\|EC\|}=\frac{\|AB\|}{\|AC\|}$

Dla powyższych rysunków zach

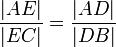
$\frac{|AE|}{|EC|}=\frac{|AD|}{|DB|}$


	$\frac{\|AE\|}{\|AC\|}=\frac{\|AD\|}{\|AB\|}$

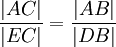
$\frac{|AC|}{|EC|}=\frac{|AB|}{|DB|}$

lub po przekształceniu:

oraz

a także

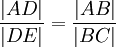
$\frac{|AD|}{|DE|}=\frac{|AB|}{|BC|}$

Często spotykaną nieścisłością jest takie formułowanie twierdzenia Talesa:

,ta równość jest oczywiście prawdziwa, ale wynika z podobieństwa trójkątów ADE i ABC a nie z samego twierdzenia Talesa.

1 1. UKŁADY RÓWNAŃ

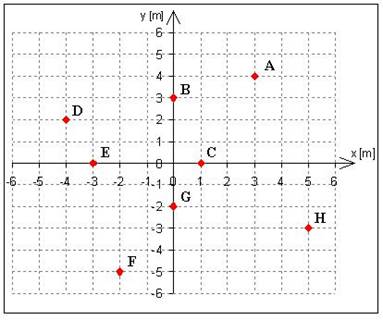
Funkcja przypisująca każdemu punktowi danej przestrzeni (w szczególności przestrzeni dwuwymiarowej – płaszczyzny, powierzchni kuli itp.)

skończony ciąg (krotkę) liczb rzeczywistych zwanych współrzędnymi punktu.

Z definicji funkcji takie przyporządkowanie pozwala jednoznacznie określić punkt na podstawie znajomości jego współrzędnych,

jednak bywa, że danemu punktowi odpowiadać może kilka współrzędnych.

Formalnie jest więc to funkcja z pewnego podzbioru Rⁿ na daną przestrzeń.

WYMIAR PRZESTRZENI

W przypadku rozmaitości topologicznych (te są najciekawsze z punktu widzenia matematyki) liczba współrzędnych niezbędnych do określenia położenia punktu jest równa wymiarowi rozmaitości.

Przykładem przestrzeni jednowymiarowej jest prosta.

Do określenia położenia na prostej wystarczy wskazać pewien punkt (początek układu) oraz określić, po której stronie tego punktu odkładane będą liczby dodatnie, a po której ujemne.

Tak zorientowaną prostą nazywamy osią liczbową.

UOGÓLNIENIE

W matematyce rozważa się przestrzenie o większej liczbie wymiarów, a także przestrzenie nieskończeniewymiarowe.

Można stosować także prostoliniowy układ współrzędnych, w którym osie nie są prostopadłe,

lub krzywoliniowy układ współrzędnych, w którym osie są krzywymi, które nie są liniami prostymi.

W ogólności, poszczególne współrzędne nie muszą być liczbami rzeczywistymi – rozważa się również współrzędne zespolone lub należące do dowolnego ciała.

LINKI DO STRON MOICH KOLEGÓW :

Łukasz P.

Jan P.

Szymon S.

LINKI DO MOICH STRON :

Darmowy hosting zapewnia PRV.PL